Nash Poker

Nash ICM calculation is the based on Nash equilibrium theory. This theory belongs on John Forbes Nash. If you remember there was a movie called A Beautiful Mind about John Nash's life. In these days, It is close to impossible to find the exact Poker Nash Equilibrium strategy for. In this case there are two pure-strategy Nash equilibria, when both choose to either drive on the left or on the right. If we admit mixed strategies (where a pure strategy is chosen at random, subject to some fixed probability), then there are three Nash equilibria for the same case: two we have seen from the pure-strategy form, where the probabilities are (0%, 100%) for player one, (0%, 100%. Going up against poker monsters while relying only on your intuition and basic knowledge of the game is tantamount to trying to stop a tank with a water gun. If you want to pose a genuine threat to professional poker players and make real money in poker tournaments, ICMIZER is an indispensable tool in your arsenal.

• Poker Nash Charts Explained
• Nash Poker Shove Chart

Poker Stack Exchange is a question and answer site for serious players and enthusiasts of poker. Nash Equilibrium is where two players don't have an incentive to. If you think about it, that means that every poker situation and poker in general has its own Nash equilibrium. In theory, if everyone plays perfectly, even no-limit hold’em is a solved game. Should we start panicking? First of all, there is a huge difference between knowing there is a Nash equilibrium and finding one.

Developed by professional poker player Max Silver, SnapShove combines unexploitable nash equilibrium ranges with an instant, easy to use and flexible interface allowing you to get the perfect play for any shove, call or reshove situation.

SnapShove’s exclusive training mode quickly puts your short stack skills to the test with the added pressure of time. These quick reflex shove, fold and call decisions are one of the best ways to massively improve your skills rapidly over time.

SnapShove is used by over 54,000 poker players worldwide including many of the worlds best. Our frequent users include WSOP Bracelet winners, Super High Roller champions and many of the world’s top 300 GPI Players.

SnapShove is available FREE with a limited number of searches per day. SnapShove pro adds unlimited searches and expert features. These include instant search and the unique “SnapShove/SnapFold” buttons letting find the perfect ranges for the next hand with a single click.

Kuhn poker is an extremely simplified form of poker developed by Harold W. Kuhn as a simple model zero-sum two-player imperfect-information game, amenable to a complete game-theoretic analysis. In Kuhn poker, the deck includes only three playing cards, for example a King, Queen, and Jack. One card is dealt to each player, which may place bets similarly to a standard poker. If both players bet or both players pass, the player with the higher card wins, otherwise, the betting player wins.

Game description[edit]

In conventional poker terms, a game of Kuhn poker proceeds as follows:

• Each player antes 1.
• Each player is dealt one of the three cards, and the third is put aside unseen.
• Player one can check or bet 1.
  • If player one checks then player two can check or bet 1.
    • If player two checks there is a showdown for the pot of 2 (i.e. the higher card wins 1 from the other player).
    • If player two bets then player one can fold or call.
      • If player one folds then player two takes the pot of 3 (i.e. winning 1 from player 1).
      • If player one calls there is a showdown for the pot of 4 (i.e. the higher card wins 2 from the other player).
  • If player one bets then player two can fold or call.
    • If player two folds then player one takes the pot of 3 (i.e. winning 1 from player 2).
    • If player two calls there is a showdown for the pot of 4 (i.e. the higher card wins 2 from the other player).

Optimal strategy[edit]

The game has a mixed-strategyNash equilibrium; when both players play equilibrium strategies, the first player should expect to lose at a rate of −1/18 per hand (as the game is zero-sum, the second player should expect to win at a rate of +1/18). There is no pure-strategy equilibrium.

Kuhn demonstrated there are infinitely many equilibrium strategies for the first player, forming a continuum governed by a single parameter. In one possible formulation, player one freely chooses the probability${\displaystyle \alpha \in [0,1/3]}$ with which he will bet when having a Jack (otherwise he checks; if the other player bets, he should always fold). When having a King, he should bet with the probability of ${\displaystyle 3\alpha }$ (otherwise he checks; if the other player bets, he should always call). He should always check when having a Queen, and if the other player bets after this check, he should call with the probability of ${\displaystyle \alpha +1/3}$.

The second player has a single equilibrium strategy: Always betting or calling when having a King; when having a Queen, checking if possible, otherwise calling with the probability of 1/3; when having a Jack, never calling and betting with the probability of 1/3.

Generalized versions[edit]

In addition to the basic version invented by Kuhn, other versions appeared adding bigger deck, more players, betting rounds, etc., increasing the complexity of the game.

3-player Kuhn Poker[edit]

A variant for three players was introduced in 2010 by Nick Abou Risk and Duane Szafron. In this version, the deck includes four cards (adding a ten card), from which three are dealt to the players; otherwise, the basic structure is the same: while there is no outstanding bet, a player can check or bet, with an outstanding bet, a player can call or fold. If all players checked or at least one player called, the game proceeds to showdown, otherwise, the betting player wins.

A family of Nash equilibria for 3-player Kuhn poker is known analytically, which makes it the largest game with more than two players with analytic solution.^[1] The family is parameterized using 4–6 parameters (depending on the chosen equilibrium). In all equilibria, player 1 has a fixed strategy, and he always checks as the first action; player 2's utility is constant, equal to –1/48 per hand. The discovered equilibrium profiles show an interesting feature: by adjusting a strategy parameter ${\displaystyle \beta }$ (between 0 and 1), player 2 can freely shift utility between the other two players while still remaining in equilibrium; player 1's utility is equal to ${\displaystyle -\frac{1+2\beta }{48}}$ (which is always worse than player 2's utility), player 3's utility is ${\displaystyle \frac{1+\beta }{24}}$.

It is not known if this equilibrium family covers all Nash equilibria for the game.

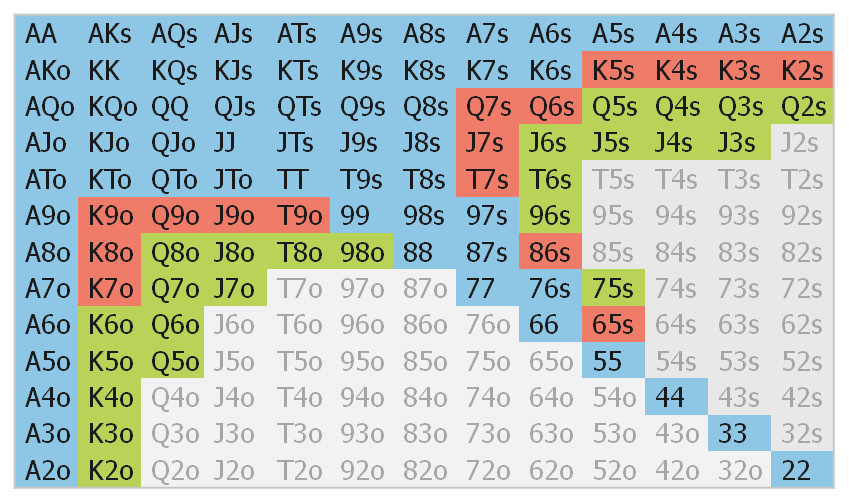
Poker Nash Charts Explained

References[edit]

• Kuhn, H. W. (1950). 'Simplified Two-Person Poker'. In Kuhn, H. W.; Tucker, A. W. (eds.). Contributions to the Theory of Games. 1. Princeton University Press. pp. 97–103.
• James Peck. 'Perfect Bayesian Equilibrium'(PDF). Ohio State University. Retrieved 2 September 2016.^:19–29

1. ^Szafron, Duane; Gibson, Richard; Sturtevant, Nathan (May 2013). 'A Parameterized Family of Equilibrium Profiles forThree-Player Kuhn Poker'(PDF). In Ito; Jonker; Gini; Shehory (eds.). Proceedings of the 12th International Conference on Autonomous Agents and Multiagent Systems (AAMAS 2013). Saint Paul, Minnesota, USA.

Nash Poker Shove Chart

External links[edit]